Diffraction
Light is a transverse electromagnetic wave. Diffraction, and interference are phenomena observed with all waves.
| Diffraction is the tendency of a wave emitted from a finite source or passing through a finite aperture to spread out as it propagates. Diffraction results from the interference of an infinite number of waves emitted by a continuous distribution of source points. According to Huygens' principle every point on a wave front of light can be considered to be a secondary source of spherical wavelets. These waveletspropagate outward with the characteristic speed of the wave. The wavelets emitted by all points on the wave front interfere with each other to produce the traveling wave. Huygens' principle also holds for electromagnetic waves. When studying the propagation of light, we can replace any wave front by a collection of sources distributed uniformly over the wave front, radiating in phase. |
| When light passes through a small opening, comparable in size to the wavelength λ of the light, in an otherwise opaque obstacle, the wave front on the other side of the opening resembles the wave front shown on the right. |
The light spreads around the edges of the obstacle. This is the phenomenon of diffraction. Diffraction is a wave phenomenon and is also observed with water waves in a ripple tank.
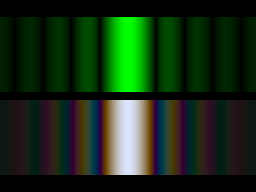
The tracks of a compact discact as a diffraction grating, producing a separation of the colors of white light. The nominal track separation on a CD is 1.6 micrometers, corresponding to about 625 tracks per millimeter. This is in the range of ordinary laboratory diffraction gratings. WAVESDiffraction of White Light (Experiment)This video serves as revision resource for my students from St Michael.Copyright of NIYNot For Sale.Not for Comme. The key to understanding why light behaves like waves is in INTERFERENCE and DIFFRACTION. Interference and Diffraction are the phenomena that distinguish waves from particles: waves interfere and diffract, particles do not. Light bends around obstacles like waves do, and it is this bending which causes the single slit diffraction pattern.
| Water waves in a ripple tank | |
A single large slit: | A single small slit: |
The single slit
| When light passes through a single slit whose width w is on the order of the wavelength of the light, then we can observe a single slit diffraction pattern on a screen that is a distance L >> w away from the slit. The intensity is a function of angle. Huygens' principle tells us that each part of the slit can be thought of as an emitter of waves. All these waves interfere to produce the diffraction pattern. Where crest meets crest we have constructive interference and where crest meets trough we have destructive interference. |
Very far from a point source the wave fronts are essentially plane waves. This is called the Fraunhofer regime, and the diffraction pattern is called Fraunhofer diffraction. The positions of all maxima and minima in the Fraunhofer diffraction pattern from a single slit can be found from the following simple arguments.
|
| If the optical path length of two rays differs by λ/2, the two rays interfere destructively. For ray 1 and ray 7 to be half a wavelength out of phase we need (w/2)sinθ = λ/2 or wsinθ = λ. But from geometry, if these two rays interfere destructively, so do rays 2 and 8, 3 and 8, and 6 and 10, 5 and 11, and 6 and 12. In effect, light from one half of the opening interferes destructively and cancels out light from the other half. Destructive interference produces the dark fringes. Dark fringes in the diffraction pattern of a single slit are found at angles θ for which w sinθ = mλ, where m is an integer, m = 1, 2, 3, .. . For the first dark fringe we have w sinθ = λ. When w is smaller than λ , the equation wsinθ = λ has no solution and no dark fringes are produced. |
| If the interference pattern is viewed on a screen a distance L from the slits, then the wavelength can be found from the spacing of the fringes. We have λ = w sinθ/m and sinθ = z/(L2 + z2)1/2), or λ = zw/(m(L2 + z2)1/2), where z is the distance from the center of the interference pattern to the mth dark line in the pattern. If L >> z then (L2 + z2)1/2 ~ L and we can write λ = zw/(mL). |
Problem:
When a monochromatic light source shines through a 0.2 mm wide slit onto a screen 3.5 m away, the first dark band in the pattern appears 9.1 mm from the center of the bright band. What is the wavelength of the light?
- Solution:
z = 9.1 mm = 9.1*10-3 m
L = 3.5 m
w = 0.2 mm = 2*10-4 m
L >> z, therefore λ = zw/(mL)
λ = (9.1*10-3 m)(2*10-4 m)/(3.5 m)
λ = 5.2*10-7 m = 520 nm
Link: Single slit diffraction II
Diffraction, and interference are phenomena observed with all waves.
- Observe single and double slit diffraction with water waves.
Interference
The double slit
| If light is incident onto an obstacle which contains two very small slits a distance d apart, then the wavelets emanating from each slit will interfere behind the obstacle. Waves passing through each slit are diffracted and spread out. At angles where the single slit diffraction pattern produces nonzero intensity, the waves from the two slits can now constructively or destructively interfere. If we let the light fall onto a screen behind the obstacle, we will observe a pattern of bright and dark stripes on the screen, in the region where with a single slit we only observe a diffraction maximum. This pattern of bright and dark lines is known as an interference fringe pattern. The bright lines indicate constructive interference and the dark lines indicate destructive interference. Metropolitan museum of art fashion. The bright fringe in the middle of the diagram on the right is caused by constructive interference of the light from the two slits traveling the same distance to the screen. It is known as the zero-order fringe. Crest meets crest and trough meets trough. The dark fringes on either side of the zero-order fringe are caused by destructive interference. Light from one slit travels a distance that is ½ wavelength longer than the distance traveled by light from the other slit. Crests meet troughs at these locations. T he dark fringes are followed by the first-order fringes, one on each side of the zero-order fringe. Light from one slit travels a distance that is one wavelength longer than the distance traveled by light from the other slit to reach these positions. Crest again meets crest. |
The diagram on the right shows the geometry for the fringe pattern. If light with wavelength λ passes through two slits separated by a distance d, we will observe constructively interference at certain angles. These angles are found by applying the condition for constructive interference, which is d sinθ = mλ, m = 0, 1, 2, … . The distances from the two slits to the screen differ by an integer number of wavelengths. Crest meets crest. The angles at which dark fringes occur can be found be applying the condition for destructive interference, which is d sinθ = (m+½)λ, m = 0, 1, 2, … . The distances from the two slits to the screen differ by an integer number of wavelengths + ½ wavelength. Crest meets trough. |
If the interference pattern is viewed on a screen a distance L from the slits, then the wavelength can be found from the spacing of the fringes.
We have sinθ = z/(L2 + z2)1/2 and λ = zd/(m(L2 + z2)1/2), where z is the distance from the center of the interference pattern to the mth bright line in the pattern.
If L >> z then (L2 + z2)1/2 ~ L and we can write
λ = zd/(mL).
Link: Physics 2000: Wave Interference
Diffraction grating
| We have seen that diffraction patterns can be produced by a single slit or by two slits. When light encounters an entire array of identical, equally-spaced slits, called a diffraction grating, the bright fringes, which come from constructive interference of the light waves from different slits, are found at the same angles they are found if there are only two slits. But the pattern is much sharper. The figure on the right shows the interference pattern for various numbers of slits. The width of all slits is 50 micrometers and the spacing between all slits is 150 micrometers. The location of the maxima for two slits is also the location of the maxima for multiple slits. The single slit pattern acts as an envelope for the multiple slit patterns. Diffraction gratings contain a large number of parallel, closely spaced slits or grooves. They produce interference maxima at angles θ given by d sinθ = mλ. Because the spacing between the slits is generally very small, the angles θ are generally quite large. We cannot use the small angle approximation for relating wavelength and the position of the maxima on a screen for gratings, but have to use sinθ = z/(L2 + z2)1/2. |
| Diffraction gratings disperse white light into its component colors because different wavelengths produce bright fringes at different angles. d sinθ = mλ, The spectral pattern is repeated on either side of the main pattern. These repetitions are called 'higher order spectra'. There are often many of them, each one fainter than the previous one. If the distance between slits is d, and the angle to a bright fringe of a particular color is θ, the wavelength of the light can be calculated. Outline Structure for Literary Analysis Essay I. Catchy Title II. Paragraph 1: Introduction (Use HATMAT) A. Main characters E. A short summary F. Paragraph 2: First Body Paragraph A. Topic sentence (what this paragraph will discuss, how it will prove your thesis) B. Context for the quote 1. Analysis essay outline. What Is An Analysis Essay? An analysis is an interpretive process that draws conclusions from a set of facts. It involves breaking down something into its various elements and asking critical thinking questions such as ‘why' and ‘how' in order to reach your own conclusions. Literary Analysis Essay Outline - A Step By Step Guide A literary analysis essay is a form of writing in which a writer examines and evaluates literature. This essay type analyzes the different components of literature by splitting it into pieces. Analyzing the different elements of the literature is not enough to draft a literary analysis essay. An analytical essay is basically an expanded five-paragraph essay containing an introduction, body, and conclusion, with specific components required for each section. Basic outline of an Analytical Essay. Introduction of Your Analytical Essay Outline The purpose of your introduction is to get the reader interested in your analysis. The introduction should include at least three things—a hook, your thesis statement, and a sentence or two describing how you intend to prove your thesis statement. |
Problem:
The first order bright line appears 0.25 cm from the center bright line when a double slit grating is used. The distance between the slits is 0.5 mm and the screen is 2.7 m from the grating. Find the wavelength.
- Solution:
z = 0.25 cm = 2.5*10-3 m
L = 2.7 m
d = 0.5 mm = 5*10-4 m
L >> z, therefore λ = zd/(mL)
λ = (2.5*10-3 m)(5*10-4 m)/(2.7 m)
λ = 4.63*10-7 m = 463 nm
Problem:
A diffraction grating has 420 lines per mm. The grating is used to observe normally incident light with a wavelength of 440 nm. The grating is placed 1.3 m from a screen. Where on the screen will the first order bright line appear?
- Solution:
d sinθ = λ
d=(1/420) mm=2.38*10-3 mm=2.38*10-6 m
λ=440 nm=4.40*10-7 m
L=1.3 m = distance to the screen.
sinθ = λ/d = 10.65o.
z= L tanq =24.5 cm = distance from the central maximum.
Diffraction patterns can be observed when light passes through a set of regularly spaced slits. For a diffraction to produce an observable pattern, the spacing of the slits must be comparable to the wavelength of the radiation. Visible light has a wavelength range from ~400 nm to ~700 nm. A typical diffraction grating for visible light with 300 grooves per mm has a slit spacing of (1/300)mm = 3 mm = 3000 nm. This spacing is 4 to 8 times larger than the wavelengths of visible light and produces an easily observable pattern.
The wavelengths of x-rays lie in the 1 nm to 1 pm range. A typical diffraction grating will not produce an observable pattern. But the wavelengths of x-rays are comparable to the spacing of atoms in common crystals, and material with a regularly spaced grid of atoms can diffract x-rays and produce diffraction patterns that can be captured on photographic film.
We classically think of light as always traveling in straight lines, but when light waves pass near a barrier they tend to bend around that barrier and become spread out. Diffraction of light occurs when a light wave passes by a corner or through an opening or slit that is physically the approximate size of, or even smaller than that light's wavelength.
The latest tweets from @TynanSylvester. Twitter rimworld.
A very simple demonstration of diffraction can be conducted by holding your hand in front of a light source and slowly closing two fingers while observing the light transmitted between them. As the fingers approach each other and come very close together, you begin to see a series of dark lines parallel to the fingers. The parallel lines are actually diffraction patterns. This phenomenon can also occur when light is 'bent' around particles that are on the same order of magnitude as the wavelength of the light. A good example of this is the diffraction of sunlight by clouds that we often refer to as a silver lining, illustrated in Figure 1 with a beautiful sunset over the ocean.
We can often observe pastel shades of blue, pink, purple, and green in clouds that are generated when light is diffracted from water droplets in the clouds. The amount of diffraction depends on the wavelength of light, with shorter wavelengths being diffracted at a greater angle than longer ones (in effect, blue and violet light are diffracted at a higher angle than is red light). As a light wave traveling through the atmosphere encounters a droplet of water, as illustrated below, it is first refracted at the water:air interface, then it is reflected as it again encounters the interface. The beam, still traveling inside the water droplet, is once again refracted as it strikes the interface for a third time. This last interaction with the interface refracts the light back into the atmosphere, but it also diffracts a portion of the light as illustrated below. This diffraction element leads to a phenomenon known as Cellini's halo (also known as the Heiligenschein effect) where a bright ring of light surrounds the shadow of the observer's head.
The terms diffraction and scattering are often used interchangeably and are considered to be almost synonymous. Diffraction describes a specialized case of light scattering in which an object with regularly repeating features (such as a diffraction grating) produces an orderly diffraction of light in a diffraction pattern. In the real world most objects are very complex in shape and should be considered to be composed of many individual diffraction features that can collectively produce a random scattering of light.
One of the classic and most fundamental concepts involving diffraction is the single-slit optical diffraction experiment, first conducted in the early nineteenth century. When a light wave propagates through a slit (or aperture) the result depends upon the physical size of the aperture with respect to the wavelength of the incident beam. This is illustrated in Figure 3 assuming a coherent, monochromatic wave emitted from point source S, similar to light that would be produced by a laser, passes through aperture d and is diffracted, with the primary incident light beam landing at point P and the first secondary maxima occurring at point Q.
As shown in the left side of the figure, when the wavelength (λ) is much smaller than the aperture width (d), the wave simply travels onward in a straight line, just as it would if it were a particle or no aperture were present. However, when the wavelength exceeds the size of the aperture, we experience diffraction of the light according to the equation:
Where θ is the angle between the incident central propagation direction and the first minimum of the diffraction pattern. The experiment produces a bright central maximum which is flanked on both sides by secondary maxima, with the intensity of each succeeding secondary maximum decreasing as the distance from the center increases. Figure 4 illustrates this point with a plot of beam intensity versus diffraction radius. Note that the minima occurring between secondary maxima are located in multiples of π.
This experiment was first explained by Augustin Fresnel who, along with Thomas Young, produced important evidence confirming that light travels in waves. From the figures above, we see how a coherent, monochromatic light (in this example, laser illumination) emitted from point L is diffracted by aperture d. Fresnel assumed that the amplitude of the first order maxima at point Q (defined as εQ) would be given by the equation:
where A is the amplitude of the incident wave, r is the distance between d and Q, and f(χ) is a function of χ, an inclination factor introduced by Fresnel.
Diffraction of Light
Explore how a beam of light is diffracted when it passes through a narrow slit or aperture. Adjust the wavelength and aperture size and observe how this affects the diffraction intensity pattern.
Diffraction White Light Vs
Diffraction of light plays a paramount role in limiting the resolving power of any optical instrument (for example: cameras, binoculars, telescopes, microscopes, and the eye). The resolving power is the optical instrument's ability to produce separate images of two adjacent points. This is often determined by the quality of the lenses and mirrors in the instrument as well as the properties of the surrounding medium (usually air). The wave-like nature of light forces an ultimate limit to the resolving power of all optical instruments.
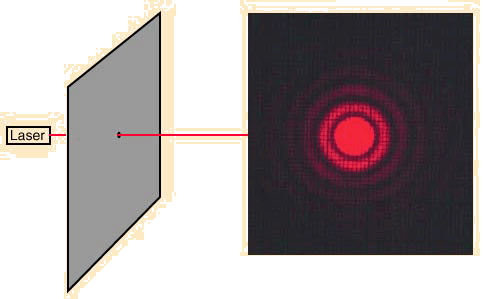
Our discussions of diffraction have used a slit as the aperture through which light is diffracted. However, all optical instruments have circular apertures, for example the pupil of an eye or the circular diaphragm and lenses of a microscope. Circular apertures produce diffraction patterns similar to those described above, except the pattern naturally exhibits a circular symmetry. Mathematical analysis of the diffraction patterns produced by a circular aperture is described by the equation:
where θ(1) is the angular position of the first order diffraction minima (the first dark ring), λ is the wavelength of the incident light, d is the diameter of the aperture, and 1.22 is a constant. Under most circumstances, the angle θ(1) is very small so the approximation that the sin and tan of the angle are almost equal yields:

Diffraction
Light is a transverse electromagnetic wave. Diffraction, and interference are phenomena observed with all waves.
| Diffraction is the tendency of a wave emitted from a finite source or passing through a finite aperture to spread out as it propagates. Diffraction results from the interference of an infinite number of waves emitted by a continuous distribution of source points. According to Huygens' principle every point on a wave front of light can be considered to be a secondary source of spherical wavelets. These waveletspropagate outward with the characteristic speed of the wave. The wavelets emitted by all points on the wave front interfere with each other to produce the traveling wave. Huygens' principle also holds for electromagnetic waves. When studying the propagation of light, we can replace any wave front by a collection of sources distributed uniformly over the wave front, radiating in phase. |
| When light passes through a small opening, comparable in size to the wavelength λ of the light, in an otherwise opaque obstacle, the wave front on the other side of the opening resembles the wave front shown on the right. |
The light spreads around the edges of the obstacle. This is the phenomenon of diffraction. Diffraction is a wave phenomenon and is also observed with water waves in a ripple tank.
The tracks of a compact discact as a diffraction grating, producing a separation of the colors of white light. The nominal track separation on a CD is 1.6 micrometers, corresponding to about 625 tracks per millimeter. This is in the range of ordinary laboratory diffraction gratings. WAVESDiffraction of White Light (Experiment)This video serves as revision resource for my students from St Michael.Copyright of NIYNot For Sale.Not for Comme. The key to understanding why light behaves like waves is in INTERFERENCE and DIFFRACTION. Interference and Diffraction are the phenomena that distinguish waves from particles: waves interfere and diffract, particles do not. Light bends around obstacles like waves do, and it is this bending which causes the single slit diffraction pattern.
| Water waves in a ripple tank | |
A single large slit: | A single small slit: |
The single slit
| When light passes through a single slit whose width w is on the order of the wavelength of the light, then we can observe a single slit diffraction pattern on a screen that is a distance L >> w away from the slit. The intensity is a function of angle. Huygens' principle tells us that each part of the slit can be thought of as an emitter of waves. All these waves interfere to produce the diffraction pattern. Where crest meets crest we have constructive interference and where crest meets trough we have destructive interference. |
Very far from a point source the wave fronts are essentially plane waves. This is called the Fraunhofer regime, and the diffraction pattern is called Fraunhofer diffraction. The positions of all maxima and minima in the Fraunhofer diffraction pattern from a single slit can be found from the following simple arguments.
|
| If the optical path length of two rays differs by λ/2, the two rays interfere destructively. For ray 1 and ray 7 to be half a wavelength out of phase we need (w/2)sinθ = λ/2 or wsinθ = λ. But from geometry, if these two rays interfere destructively, so do rays 2 and 8, 3 and 8, and 6 and 10, 5 and 11, and 6 and 12. In effect, light from one half of the opening interferes destructively and cancels out light from the other half. Destructive interference produces the dark fringes. Dark fringes in the diffraction pattern of a single slit are found at angles θ for which w sinθ = mλ, where m is an integer, m = 1, 2, 3, .. . For the first dark fringe we have w sinθ = λ. When w is smaller than λ , the equation wsinθ = λ has no solution and no dark fringes are produced. |
| If the interference pattern is viewed on a screen a distance L from the slits, then the wavelength can be found from the spacing of the fringes. We have λ = w sinθ/m and sinθ = z/(L2 + z2)1/2), or λ = zw/(m(L2 + z2)1/2), where z is the distance from the center of the interference pattern to the mth dark line in the pattern. If L >> z then (L2 + z2)1/2 ~ L and we can write λ = zw/(mL). |
Problem:
When a monochromatic light source shines through a 0.2 mm wide slit onto a screen 3.5 m away, the first dark band in the pattern appears 9.1 mm from the center of the bright band. What is the wavelength of the light?
- Solution:
z = 9.1 mm = 9.1*10-3 m
L = 3.5 m
w = 0.2 mm = 2*10-4 m
L >> z, therefore λ = zw/(mL)
λ = (9.1*10-3 m)(2*10-4 m)/(3.5 m)
λ = 5.2*10-7 m = 520 nm
Link: Single slit diffraction II
Diffraction, and interference are phenomena observed with all waves.
- Observe single and double slit diffraction with water waves.
Interference
The double slit
| If light is incident onto an obstacle which contains two very small slits a distance d apart, then the wavelets emanating from each slit will interfere behind the obstacle. Waves passing through each slit are diffracted and spread out. At angles where the single slit diffraction pattern produces nonzero intensity, the waves from the two slits can now constructively or destructively interfere. If we let the light fall onto a screen behind the obstacle, we will observe a pattern of bright and dark stripes on the screen, in the region where with a single slit we only observe a diffraction maximum. This pattern of bright and dark lines is known as an interference fringe pattern. The bright lines indicate constructive interference and the dark lines indicate destructive interference. Metropolitan museum of art fashion. The bright fringe in the middle of the diagram on the right is caused by constructive interference of the light from the two slits traveling the same distance to the screen. It is known as the zero-order fringe. Crest meets crest and trough meets trough. The dark fringes on either side of the zero-order fringe are caused by destructive interference. Light from one slit travels a distance that is ½ wavelength longer than the distance traveled by light from the other slit. Crests meet troughs at these locations. T he dark fringes are followed by the first-order fringes, one on each side of the zero-order fringe. Light from one slit travels a distance that is one wavelength longer than the distance traveled by light from the other slit to reach these positions. Crest again meets crest. |
The diagram on the right shows the geometry for the fringe pattern. If light with wavelength λ passes through two slits separated by a distance d, we will observe constructively interference at certain angles. These angles are found by applying the condition for constructive interference, which is d sinθ = mλ, m = 0, 1, 2, … . The distances from the two slits to the screen differ by an integer number of wavelengths. Crest meets crest. The angles at which dark fringes occur can be found be applying the condition for destructive interference, which is d sinθ = (m+½)λ, m = 0, 1, 2, … . The distances from the two slits to the screen differ by an integer number of wavelengths + ½ wavelength. Crest meets trough. |
If the interference pattern is viewed on a screen a distance L from the slits, then the wavelength can be found from the spacing of the fringes.
We have sinθ = z/(L2 + z2)1/2 and λ = zd/(m(L2 + z2)1/2), where z is the distance from the center of the interference pattern to the mth bright line in the pattern.
If L >> z then (L2 + z2)1/2 ~ L and we can write
λ = zd/(mL).
Link: Physics 2000: Wave Interference
Diffraction grating
| We have seen that diffraction patterns can be produced by a single slit or by two slits. When light encounters an entire array of identical, equally-spaced slits, called a diffraction grating, the bright fringes, which come from constructive interference of the light waves from different slits, are found at the same angles they are found if there are only two slits. But the pattern is much sharper. The figure on the right shows the interference pattern for various numbers of slits. The width of all slits is 50 micrometers and the spacing between all slits is 150 micrometers. The location of the maxima for two slits is also the location of the maxima for multiple slits. The single slit pattern acts as an envelope for the multiple slit patterns. Diffraction gratings contain a large number of parallel, closely spaced slits or grooves. They produce interference maxima at angles θ given by d sinθ = mλ. Because the spacing between the slits is generally very small, the angles θ are generally quite large. We cannot use the small angle approximation for relating wavelength and the position of the maxima on a screen for gratings, but have to use sinθ = z/(L2 + z2)1/2. |
| Diffraction gratings disperse white light into its component colors because different wavelengths produce bright fringes at different angles. d sinθ = mλ, The spectral pattern is repeated on either side of the main pattern. These repetitions are called 'higher order spectra'. There are often many of them, each one fainter than the previous one. If the distance between slits is d, and the angle to a bright fringe of a particular color is θ, the wavelength of the light can be calculated. Outline Structure for Literary Analysis Essay I. Catchy Title II. Paragraph 1: Introduction (Use HATMAT) A. Main characters E. A short summary F. Paragraph 2: First Body Paragraph A. Topic sentence (what this paragraph will discuss, how it will prove your thesis) B. Context for the quote 1. Analysis essay outline. What Is An Analysis Essay? An analysis is an interpretive process that draws conclusions from a set of facts. It involves breaking down something into its various elements and asking critical thinking questions such as ‘why' and ‘how' in order to reach your own conclusions. Literary Analysis Essay Outline - A Step By Step Guide A literary analysis essay is a form of writing in which a writer examines and evaluates literature. This essay type analyzes the different components of literature by splitting it into pieces. Analyzing the different elements of the literature is not enough to draft a literary analysis essay. An analytical essay is basically an expanded five-paragraph essay containing an introduction, body, and conclusion, with specific components required for each section. Basic outline of an Analytical Essay. Introduction of Your Analytical Essay Outline The purpose of your introduction is to get the reader interested in your analysis. The introduction should include at least three things—a hook, your thesis statement, and a sentence or two describing how you intend to prove your thesis statement. |
Problem:
The first order bright line appears 0.25 cm from the center bright line when a double slit grating is used. The distance between the slits is 0.5 mm and the screen is 2.7 m from the grating. Find the wavelength.
- Solution:
z = 0.25 cm = 2.5*10-3 m
L = 2.7 m
d = 0.5 mm = 5*10-4 m
L >> z, therefore λ = zd/(mL)
λ = (2.5*10-3 m)(5*10-4 m)/(2.7 m)
λ = 4.63*10-7 m = 463 nm
Problem:
A diffraction grating has 420 lines per mm. The grating is used to observe normally incident light with a wavelength of 440 nm. The grating is placed 1.3 m from a screen. Where on the screen will the first order bright line appear?
- Solution:
d sinθ = λ
d=(1/420) mm=2.38*10-3 mm=2.38*10-6 m
λ=440 nm=4.40*10-7 m
L=1.3 m = distance to the screen.
sinθ = λ/d = 10.65o.
z= L tanq =24.5 cm = distance from the central maximum.
Diffraction patterns can be observed when light passes through a set of regularly spaced slits. For a diffraction to produce an observable pattern, the spacing of the slits must be comparable to the wavelength of the radiation. Visible light has a wavelength range from ~400 nm to ~700 nm. A typical diffraction grating for visible light with 300 grooves per mm has a slit spacing of (1/300)mm = 3 mm = 3000 nm. This spacing is 4 to 8 times larger than the wavelengths of visible light and produces an easily observable pattern.
The wavelengths of x-rays lie in the 1 nm to 1 pm range. A typical diffraction grating will not produce an observable pattern. But the wavelengths of x-rays are comparable to the spacing of atoms in common crystals, and material with a regularly spaced grid of atoms can diffract x-rays and produce diffraction patterns that can be captured on photographic film.
We classically think of light as always traveling in straight lines, but when light waves pass near a barrier they tend to bend around that barrier and become spread out. Diffraction of light occurs when a light wave passes by a corner or through an opening or slit that is physically the approximate size of, or even smaller than that light's wavelength.
The latest tweets from @TynanSylvester. Twitter rimworld.
A very simple demonstration of diffraction can be conducted by holding your hand in front of a light source and slowly closing two fingers while observing the light transmitted between them. As the fingers approach each other and come very close together, you begin to see a series of dark lines parallel to the fingers. The parallel lines are actually diffraction patterns. This phenomenon can also occur when light is 'bent' around particles that are on the same order of magnitude as the wavelength of the light. A good example of this is the diffraction of sunlight by clouds that we often refer to as a silver lining, illustrated in Figure 1 with a beautiful sunset over the ocean.
We can often observe pastel shades of blue, pink, purple, and green in clouds that are generated when light is diffracted from water droplets in the clouds. The amount of diffraction depends on the wavelength of light, with shorter wavelengths being diffracted at a greater angle than longer ones (in effect, blue and violet light are diffracted at a higher angle than is red light). As a light wave traveling through the atmosphere encounters a droplet of water, as illustrated below, it is first refracted at the water:air interface, then it is reflected as it again encounters the interface. The beam, still traveling inside the water droplet, is once again refracted as it strikes the interface for a third time. This last interaction with the interface refracts the light back into the atmosphere, but it also diffracts a portion of the light as illustrated below. This diffraction element leads to a phenomenon known as Cellini's halo (also known as the Heiligenschein effect) where a bright ring of light surrounds the shadow of the observer's head.
The terms diffraction and scattering are often used interchangeably and are considered to be almost synonymous. Diffraction describes a specialized case of light scattering in which an object with regularly repeating features (such as a diffraction grating) produces an orderly diffraction of light in a diffraction pattern. In the real world most objects are very complex in shape and should be considered to be composed of many individual diffraction features that can collectively produce a random scattering of light.
One of the classic and most fundamental concepts involving diffraction is the single-slit optical diffraction experiment, first conducted in the early nineteenth century. When a light wave propagates through a slit (or aperture) the result depends upon the physical size of the aperture with respect to the wavelength of the incident beam. This is illustrated in Figure 3 assuming a coherent, monochromatic wave emitted from point source S, similar to light that would be produced by a laser, passes through aperture d and is diffracted, with the primary incident light beam landing at point P and the first secondary maxima occurring at point Q.
As shown in the left side of the figure, when the wavelength (λ) is much smaller than the aperture width (d), the wave simply travels onward in a straight line, just as it would if it were a particle or no aperture were present. However, when the wavelength exceeds the size of the aperture, we experience diffraction of the light according to the equation:
Where θ is the angle between the incident central propagation direction and the first minimum of the diffraction pattern. The experiment produces a bright central maximum which is flanked on both sides by secondary maxima, with the intensity of each succeeding secondary maximum decreasing as the distance from the center increases. Figure 4 illustrates this point with a plot of beam intensity versus diffraction radius. Note that the minima occurring between secondary maxima are located in multiples of π.
This experiment was first explained by Augustin Fresnel who, along with Thomas Young, produced important evidence confirming that light travels in waves. From the figures above, we see how a coherent, monochromatic light (in this example, laser illumination) emitted from point L is diffracted by aperture d. Fresnel assumed that the amplitude of the first order maxima at point Q (defined as εQ) would be given by the equation:
where A is the amplitude of the incident wave, r is the distance between d and Q, and f(χ) is a function of χ, an inclination factor introduced by Fresnel.
Diffraction of Light
Explore how a beam of light is diffracted when it passes through a narrow slit or aperture. Adjust the wavelength and aperture size and observe how this affects the diffraction intensity pattern.
Diffraction White Light Vs
Diffraction of light plays a paramount role in limiting the resolving power of any optical instrument (for example: cameras, binoculars, telescopes, microscopes, and the eye). The resolving power is the optical instrument's ability to produce separate images of two adjacent points. This is often determined by the quality of the lenses and mirrors in the instrument as well as the properties of the surrounding medium (usually air). The wave-like nature of light forces an ultimate limit to the resolving power of all optical instruments.
Our discussions of diffraction have used a slit as the aperture through which light is diffracted. However, all optical instruments have circular apertures, for example the pupil of an eye or the circular diaphragm and lenses of a microscope. Circular apertures produce diffraction patterns similar to those described above, except the pattern naturally exhibits a circular symmetry. Mathematical analysis of the diffraction patterns produced by a circular aperture is described by the equation:
where θ(1) is the angular position of the first order diffraction minima (the first dark ring), λ is the wavelength of the incident light, d is the diameter of the aperture, and 1.22 is a constant. Under most circumstances, the angle θ(1) is very small so the approximation that the sin and tan of the angle are almost equal yields:
From these equations it becomes apparent that the central maximum is directly proportional to λ/d making this maximum more spread out for longer wavelengths and for smaller apertures. The secondary mimina of diffraction set a limit to the useful magnification of objective lenses in optical microscopy, due to inherent diffraction of light by these lenses. No matter how perfect the lens may be, the image of a point source of light produced by the lens is accompanied by secondary and higher order maxima. This could be eliminated only if the lens had an infinite diameter. Two objects separated by a distance less than θ(1) can not be resolved, no matter how high the power of magnification. While these equations were derived for the image of a point source of light an infinite distance from the aperture, it is a reasonable approximation of the resolving power of a microscope when d is substituted for the diameter of the objective lens.
Thus, if two objects reside a distance D apart from each other and are at a distance L from an observer, the angle (expressed in radians) between them is:
which leads us to be able to condense the last two equations to yield:
Where D(0) is the minimum separation distance between the objects that will allow them to be resolved. Using this equation, the human eye can resolve objects separated by a distance of 0.056 millimeters, however the photoreceptors in the retina are not quite close enough together to permit this degree of resolution, and 0.1 millimeters is a more realistic number under normal circumstances.
The resolving power of optical microscopes is determined by a number of factors including those discussed, but in the most ideal circumstances, this number is about 0.2 micrometers. This number must take into account optical alignment of the microscope, quality of the lenses, as well as the predominant wavelengths of light used to image the specimen. While it is often not necessary to calculate the exact resolving power of each objective (and would be a waste of time in most instances), it is important to understand the capabilities of the microscope lenses as they apply to the real world.
Diffraction White Light Spectrum
Contributing Authors
Mortimer Abramowitz - Olympus America, Inc., Two Corporate Center Drive., Melville, New York, 11747.
White-light Diffraction Tomography Of Unlabelled Live Cells
Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.

